MATLAB Lesson 10 - Log scale plots

Resources

print print this page

When dealing with very large values or very small positive values, it is useful to plot data or functions using a log scale. A log scale can be used either on the x-axis, or the y-axis or both.

Y-axis log scale

To create a plot with a linear scale on the x-axis and a log (base 10) scale on the y-axis you can use the function semilogy.

The limit as k goes to infinity of ak = (1 + r/k)k is er. To illustrate this plot the errors ek = | er - ak | against k for k = 1,...,100.

Define a value for r

Define a vector K of integers from 1 to 100

Define the elements of the sequence using element by element division ./ and element by element powers .^

Define the vector of magnitudes of the errors

In the first subplot use a linear scale on both axes.

 

In the second subplot use a log scale for the y-axis.

>>  r = 0.06;
>>  K = [1:100];
>>  A = (1 + r./K).^K;
>>  E = abs(exp(r) - A);
>>  subplot(2,1,1)
>>  plot(K, E)
>>  subplot(2,1,2)
>>  semilogy(K, E)


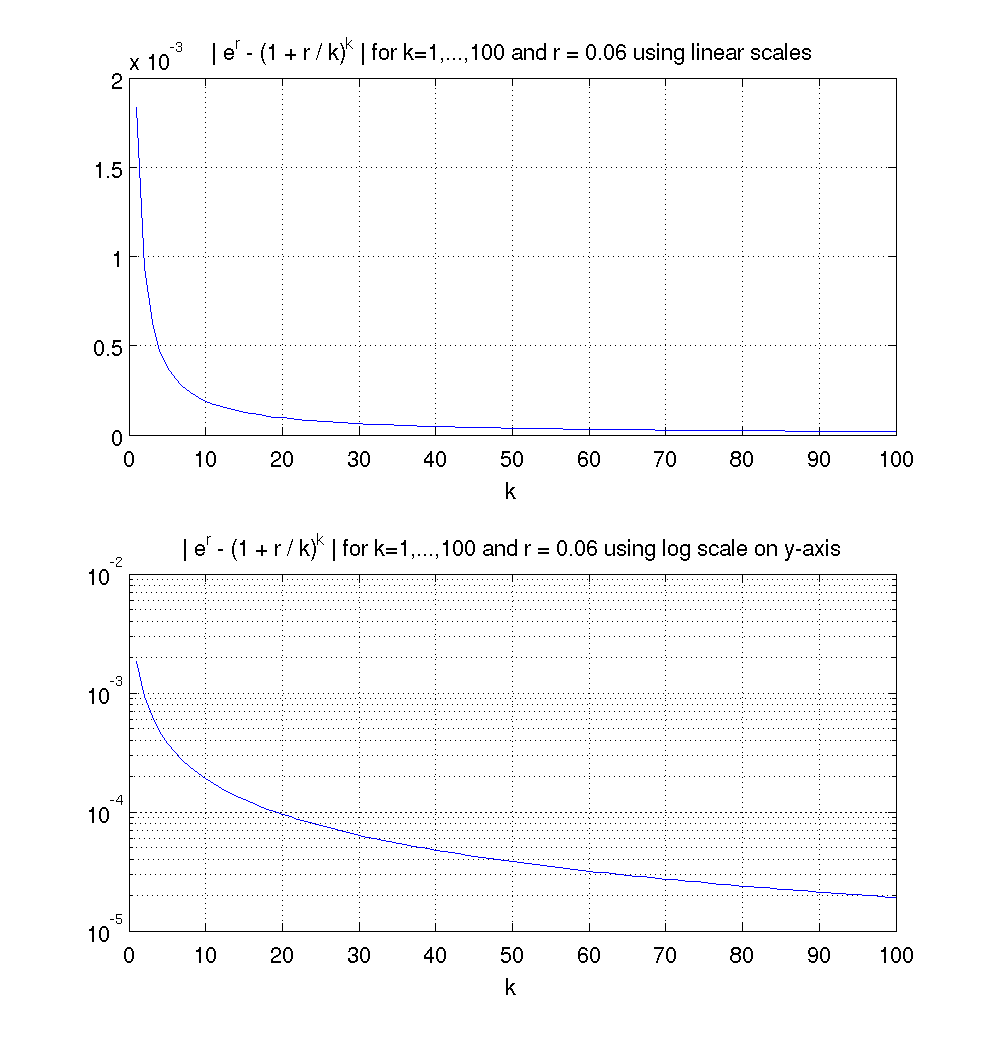
experr

The MATLAB M-file used to create this plot is experr.m.

X-axis log scale

To create a plot with a linear scale on the x-axis and a log (base 10) scale on the x-axis you can use the function semilogx.

 

Log scale on both axes

To create a plot using a log (base 10) scale for both the x-axis and and the y-axis you can use the function loglog.

Plot the values k-0.4 for k = 1, 4, 9, ... 1002 using linear scales on both axes, a log scale on the x-axis and log scales on both axes. Which plot most clearly illustrates the exponent -0.4?

Create a vector K of the values 1, 4, 9, ..., 1002.

Create a vector Y of the values.

Create a figure with 3 subplots.

The first subplot uses a linear scale for both axes.

The second subplot uses a log scale for the x-axes.

The third subplot uses a log scale for both axes.

>>  K = [1:100].^2;
>>  Y = K.^(-0.4);
>>  subplot(3,1,1);
>>  plot(K, Y);
>>  subplot(3,1,2);
>>  semilogx(K, Y);
>>  subplot(3,1,3);
>>  loglog(K, Y);

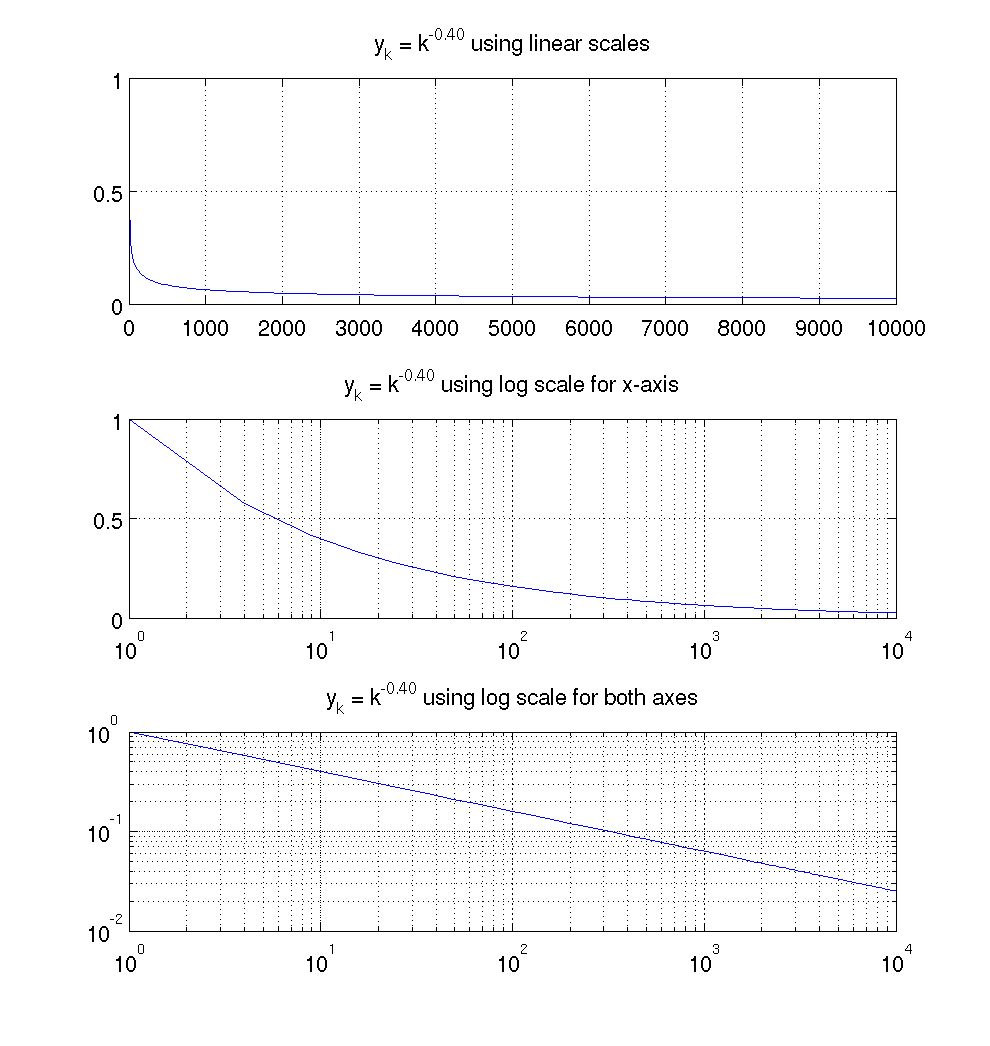
logplots

The MATLAB M-file used to create this plot is logplots.m.

 

Warnings

 

Self-test Exercise

Stirling's formula states that f(n) = log(n!) converges to g(n) = n log(n) - n as n goes to infinity.
Which Matlab function gives a scaling of the axes that produces the most information about the following functions?
  • f(n) and g(n) for n = 1,...,105
  • (f(n)-g(n)/n for n = 1,...,105
  • h(x) = x-x for x in [0, 106]

Answer:

  • loglog
  • semilogy or loglog
  • semilogx

Use the mouse to select the text between the word "Answer" and here to see the answer.

Summary

A plot with a log (base 10) scale on the x-axis (semilogx), on the y-axis (semilogy) or both axes (loglog), can be very useful when plotting very large or very small (positive) values.